Click here to download this worksheet as nicely formatted Acrobat file (pdf)

Kinetic Energy Basics
1. What is the kinetic energy of a 80 kg football player running at 8 m/s?
2. What is the kinetic energy of a 0.01 kg dart that is thrown at 20 m/s?
3. What is the kinetic energy of the space shuttle (mass = 68,000 kg) when it is orbiting the Earth at 13,000 m/s?
4. What is the kinetic energy of a bolt (0.002 kg) -lost off the space shuttle in a previous flight- floating in space at 13,000 m/s?
5. If the bolt lost off the space shuttle above hit a astronaut at 13,000 m/s, it would feel like a 105 kg running at what velocity? (Hint: Use energy to solve.)
6. What is the kinetic energy of a 20,000 kg locomotive traveling at 2 m/s?
7. How fast must a 0.0050 kg bullet travel if it is to have the same kinetic energy as a 20,000 kg locomotive traveling at 2 m/s?
8. How does the kinetic energy change if a car’s mass changes by a factor of 1/4?
9. How does the kinetic energy change if a car’s mass changes by a factor of 1/3 and changes its speed by a factor of 4/3?
10. The kinetic energy of a bicyclist changes by a factor of 2 while his velocity changes by a factor of 2. What factor did the rider's mass change by?
11. By what factor did the velocity change by if the kinetic energy changed by a factor of 7/5 and the mass changed by a factor of 7/8?
12. How must the velocity change if the kinetic energy is to be quadrupled, and the mass changed by a factor of 4/6?
13. How must the velocity change if the kinetic energy is to be tripled, and the mass changed by a factor of 2/5?
Gravitational Potential Energy Basics
14. A 7.3 kg gallon paint can is lifted 1.78 meters vertically to a shelf. What is the change in potential energy of the paint can?
15. A roller coaster car of mass 465 kg rolls up a hill with a vertical height of 75 m from the ground. What is the change in potential energy relative to the ground?
16. A 783 kg elevator rises straight up 164 meters. What is the change in potential energy of the elevator relative to the ground?
17. A car coasts 62.2 meters along a hill that makes a 28.3° angle with the ground. If the car's mass is 1234 kg, then what is the change in potential energy?

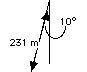
18. A mountain climber scales a cliff that makes a 10 degree angle with the vertical. The climber climbs 231 meters up along the cliff. What is the change in potential energy relative to the ground of the 823.2 Newton mountain climber?
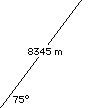
19. A 18,000 kg jet, the F/A-18 "Hornet," climbs up at 75° angle with the ground. The F/A-18 travels a distance of 8345 m. What is the change in potential energy of the F/A-18.

Conservation of Potential and Kinetic Energy
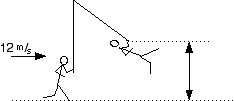
23 How fast is the bicyclist traveling at the bottom of the hill?
24a How fast is the bicyclist traveling when she jumps off the ramp at 4 m?
24b What is the maximum vertical height the bicyclist will reach?
25 What is the highest height Tarzan can travel to given the information above?
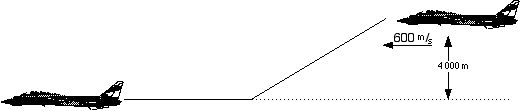
26 What is the jet’s new velocity if it coasts to its new, lower, altitude?
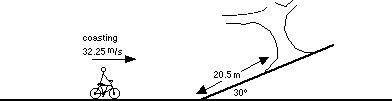
27 The question has been removed due to technica problems.
28 A bicyclist is coasting on level ground at 32.25 m/s. The bicyclist coasts up an incline and grabs an overhanging tree limb. How fast is the bicyclist traveling when he grabs the limb?
29. What is the velocity of the dropped package after falling 1500 m?

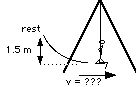
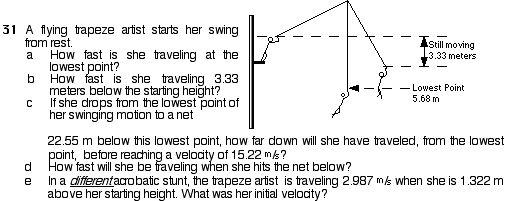
30. What is the velocity of the rider at the bottom of the swing?
Conservation of Kinetic and Potential Energy
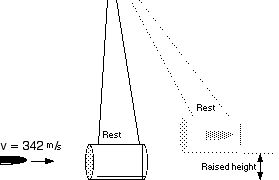
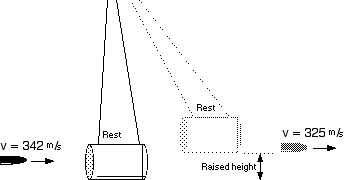
A bullet is shot into a can filled with 19.880 kg of clay. The filled can is tied to the end of a string so that it can act like a pendulum. The bullet (mass = 0.012 kg) is traveling 342 m/s before it impacts the clay filled can.
32. What is the mass of the can-bullet combination after the bullet strikes the can?
33. What is the kinetic energy of the bullet before it strikes the can?
34. What is the kinetic energy of the can-bullet when the can is raised to its maximum height?
35. What is the potential energy due to gravity when the can is at its maximum height?
36. What is the maximum height of the can?

A bullet is shot into a can filled with 19.88 kg of clay. The filled can is tied to the end of a string so that it can act like a pendulum. The bullet (mass = 0.012 kg) is traveling 342 m/s before it impacts the clay filled can. The bullet passes through the can. The bullet exits the back of the can at 325 m/s.
37 What is the maximum height of the can?

A roller coaster car, 500 kg, is to travel from 8 m/s down a wavy hill. It will coast without friction. Near the end of the ride it will make a death defying jump.
38. What is the total energy of the system at the top of the hill?
39. What is the total energy of the system at the bottom of the hill?
40. What is the speed of the car at a height of 30 m.
41. What is the speed of the cat at the bottom of the hill?
42. What is the speed of the car after landing on the 15 m hill?
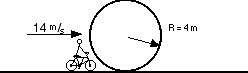
43 How many g’s does the rider feel as he enters the loop?
44 How fast is the rider traveling at the top of the loop?
45 How many g’s does the rider feel at the top of the loop?
46 Later a different rider travels into the loop at a different velocity. The rider feels 4.5 g’s at the bottom of the loop as they enter it. How fast were they traveling?

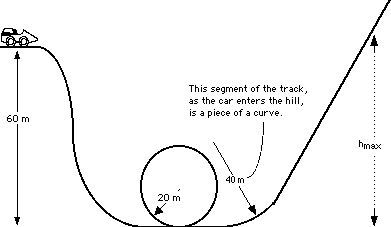
A roller coaster rolls over the top of a hill with a speed of 10 m/s. The roller coaster’s mass is 500 kg. (Ignore friction)
47. What is the speed of the roller coaster car half way down the hill?
48. What is the speed of the roller coaster car at the bottom of the hill?
49. What is the speed of the roller coaster car as it enters the loop?
50. How many g’s are felt by the rider as they enter the loop?
51. What is the speed of the roller coaster car when it is 10 m above the ground?
52. What is the speed of the roller coaster car at the top of the loop?
53. How many g’s are felt by the rider at the top of the loop?
54. What is the speed of the rider at the bottom of the loop?
55. What is the speed of the rider as they enter the hill’s curve?
56. How many g’s are felt by the rider as they enter this part of the curve?
57. How high will the roller coaster travel until it comes to a stop?
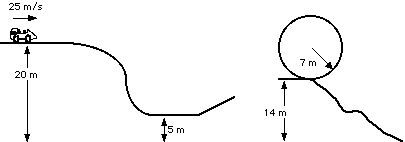
58. How fast is the car traveling after rolling down the hill to the 5 m mark?
59. How fast is the car traveling after making the jump up to 14 m?
60. How fast is the car traveling as it enters the loop?
61. What is the centripetal acceleration at this point in the loop?
62. How many g’s does the rider feel at the bottom of the loop?
63.How fast is the car traveling at the top of the loop?
64. What is the centripetal acceleration at this point in the loop?
65. How many g’s does the rider feel at the top of the loop?
66. How fast is the car traveling at the very bottom?
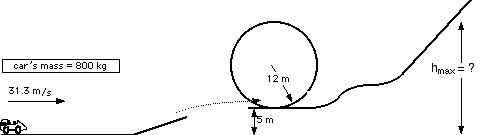
The 800 kg roller coaster car begins the run traveling 31.3 m/s. It makes the jump and travels around the loop before going up the hill at the end. The coaster rolls up the hill until it comes to a rest. from their it rolls backwards through the ride.
67. How fast is the car traveling after completing the jump?
68. How fast if the car traveling when is enters the loop?
69. How fast is the car traveling at the top of the loop?
70. What is the centripetal acceleration at top of the loop?
71. How many g’s is the centripetal acceleration at top of the loop?
72. How many g’s does the rider FEEL at the top of the loop?
73. How fast is the rider traveling at the bottom of the loop?
74. What is the centripetal acceleration at the bottom of the loop assuming the car is still barely in the loop?
75. How many g’s is the centripetal acceleration at the bottom of the loop assuming the car is still barely in the loop?
76. How many g’s does the rider FEEL at the bottom of the loop assuming the car is still barely in the loop?
77. What is the maximum height the car rolls up the hill?

78 A dog pulls a 40 kg wagon with a force of 300 N over distance of 50 m. How much work was done by the dog?
79 A car exerts a force of 10,000 N while driving on a horizontal stretch of road. How much work is done when the car travels 100 m?
80 A bucket is lifted out of a well by a 200 N force. If the well is 30 m deep, then how much work is done in lifting the bucket?
81 A 60,000 kg jet exerts a force of 1,000,000 N over a distance of 70 m. How much work is done by the jet?
82 A runner exerts 2,000 J of work while traveling 10 m along a horizontal stretch of track. How much force was exerted by the runner?
83 In order to insert a nerf dart into a toy gun, 50 J of energy needed to be exerted. It the dart was inserted 6 cm, then how much force was required to install the nerf dart?
84 A bicyclist exerted 30,000 J of work while traveling with a force of 10,000 N. How much distance was covered by the bicyclist?
85 A 1200 kg car is pushed by 3 people. Each person pushes with a force of 500 N. If the car is pushed 100 m, then how much work is done?
86 A St. Bernard dog pulls a 20 kg sled 50 meters with a 300 N force. the force act parallel to the ground. How much work does the dog do?
87 A 1500 kg does 20,000 J of work when is travels 200 m. How much force did the car exert, if the force acts parallel to the ground?
88 A model rocket exerted 1200 J of work in flight. If the rocket exerted 2 N of force, what is the maximum height the rocket can reach, without air resistance?
89 How much work is done by pushing a 100 kg box 5 m across a floor by a 20 N force?
90 How much work is done by a 500 N force that pushes a 1200 kg car 50 m if the car is moving 20 m/s when the force is applied? (The force is applied in the direction of motion.)
91 2000 J of work is done in running 50 meters. What average force is exerted by the runner?
92 A bullet penetrates 30 cm below the surface of water. If 2940 J of work is used to stop the bullet, then what is the stopping force. Ignore the effects of gravity?
93 A box is pushed by a 600 N force that acts at a 30° angle with the ground. The force pushes a 500 N box 10 meters from rest. How much work is done?
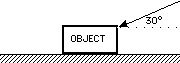
94 A 80 kg water skier is being towed behind a speed boat as shown to the right. The 600 kg boat travels 400 m. At the beginning of the run the boat is traveling 5 m/s. The force in the tether line is 2000 N. The boat travels with a net force of 4000 N. How much work is done by the tether on the skier?
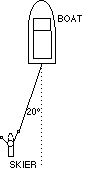
95 A 100 kg dock worker pushes a 50 kg box across a floor. He pushes the box such that his arms are at an angle as shown below. How much work is done by the person on the box?
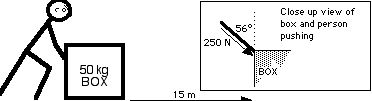
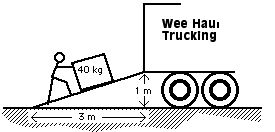
96 An 80 kg trucker loads a crate as shown below. He pushes the 40 kg box such that his arms are parallel to the ground. He pushes with a 100 N force. How much work is done by the trucker on the box?
97 Sidney, 60 kg, on a walk-about with his pet snake Cecil. Cecil’s weight is 5 kg. Cecil is pulling Sidney with 40 N force. The two travel a across a distance of 125 m. They start their trip from rest. How much work is done by Cecil?
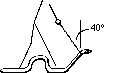
98 A 120 N sled & rider is pulled by a 200 N for 100 m. The force acts at a 60° angle with the ground. How much work is done by the applied force?
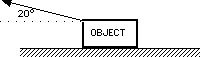
99 A 175 kg bob-sled is stopped by a force applied at a 20° angle with the ground. The sled is stopped in 25 m with 800 J of work. What is the magnitude of the force?

A musket ball, 0.20kg, is shot with a speed of 313 m/s into a metal can holding some clay. The musket ball penetrates 13.4 cm into the clay before coming to a stop.

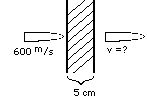
100 What is the kinetic energy of the musket ball before it hits the clay if its mass is 0.20 kg?
101 How much work does the clay do in stopping the musket ball?
102 What average force does the clay exert in stopping the musket ball?
103 Using your answer in the previous problem, calculate the speed of the musket ball when it has penetrated the clay only 4.3 and 9.8 cm.
104 A 1500 kg does 20,000 J of work when it accelerates across 200 m. The car starts from 20 m/s before traveling the 200 m. What is the final velocity of the car?

105 A 50 kg runner exerts 500 J of work while accelerating to a final velocity of 10 m/s in 50 m. What was the runner’s initial velocity?
106 A bullet, 10 g, is shot through a piece of wood. The bullet enter the wood at 600 m/s. The wood is 5 cm thick. The wood exerts 10,000 N of force to slow the bullet down. How fast is the bullet traveling when it leaves the piece of wood on the opposite side?
107 An 800 kg dragster finishes the race with some unknown velocity. A parachute is deployed after crossing the finish line and exerts a stopping force of 20,000 N across a distance of 300 m before the dragster slows down to 20 m/s. What was the speed of the dragster when it passes the finish line.

108 A bicycle stunt rider, 100.00 kg, is about to make a great jump over some busses. His bicycle exerts a force of 5,000 N in the direction of motion. He pedals along the entire distance shown. Given the diagram below, how fast will he be traveling when he leaves the ramp?


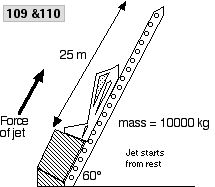
Wile E. Coyote is at it again. This time he is in a rocket boosted glider.
109 How much force is exerted by the boost motor if the glider is to leave the launch tower at 100 m/s?
110 How fast is the glider going to leave the launch tower if the glider’s boost motor exerts 5,000,000 J of work?
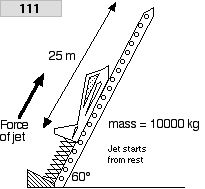
111 The Coyote is not having much success. So he trades in the glider for a jet. His launcher will now propel him using the spring and the force of the jet’s engines. The spring is compressed 25 meters along the launch tower and it’s force constant is 75,000 N/m. If the engine exerts a constant force of 90,000 N, then what is the velocity of the jet when it leaves the launch tower?
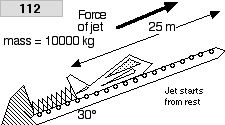
112 Suppose the the launcher is at a 30° with the ground and the jet motor exerts the same force. What is the velocity of the plane as it leaves the ramp? (It is using the same spring as stated in the previous problem.)

746 watts = 1 horsepower (hp)
113 A 2800 kg car exerts a constant force of 20,000 N while traveling across 50 m. The car starts from rest.
(a) How much work is done by the car?
(b) How much power is exerted by the car, in watts and horsepower?
114 A student lifts a bucket with a 98 N force in 30 seconds out of a well. If the bucket is lifted 30 m then;
(a) How much work is done on the bucket by the student?
(b) How much power is exerted by the student, in watts and horsepower?
115 A car 2400 kg is traveling down the road at 26.1 m/s. If the car accelerates up to 35 m/s over a distance of 200 m then
(a) How much work is done by the car?
(b) How much power is exerted by the car, in watts and horsepower?
116 After accelerating, the car mentioned in the previous problem now locks the brakes and skids to a stop in 350 m.
(a) How much work is done by the brakes?
(b) How much power is exerted by the car’s brakes, in watts and horsepower?
117 A 1400 kg car travels up a 20° incline. The car exerts a constant force of 30,000 N across 100 m. The car starts from rest at the bottom of the incline.
(a) How much work is done?
(b) How much power is exerted by the car, in watts and horsepower?
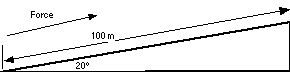
118 A 0.050 kg arrow is accelerated by the bow from rest to a velocity of 140 m/s in 0.60 m.
(a) How much work is done by the bow?
(b) How much power is exerted by the bow?
119 A 30 g toy car exerts a constant force of 4 N while traveling over the hill shown below.
(a) How much work is done by the car?
(b) How much power is exerted by the car?

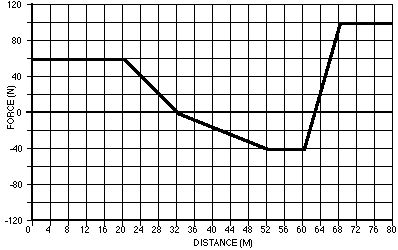
120. What is the work done over the first 12 meters?
121. What is the work done over the first 24 meters?
122. What is the work done over the first 32 meters?
123. What is the work done over the first 52 meters?
124. How much work is done between 32 and 52 meters?
125 How much energy is stored in the sling shot launcher when it is pulled back 30 cm?
126 How much energy is stored in the sling shot launcher when it pulled back 60 cm?
127 How much energy is storer in the sling shot launcher when it is pulled back 80 cm?
128 IF the plane was pulled back 80 cm and it held horizontally -not like the above picture- then how fast would it leave the launcher?
129 If the plane were pulled back 80 cm and was held like the picture above, How fast would it leave the launcher?
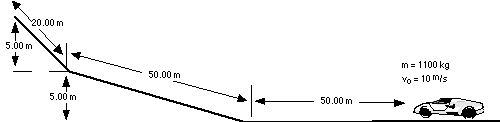
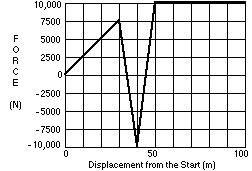
130 What is the car’s speed after traveling 30 m?
131 What is the car’s speed after traveling 50 m?
132 What is the car’s speed after traveling 100 m?
133 What is the car’s speed after traveling 120 m?
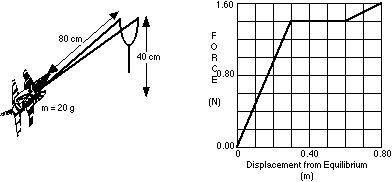
A toy plane of mass is placed on a hand held launcher. The plane is pressed against a spring until it reaches the handle. Below is a force versus displacement graph for when the plane is compressed to the handle.
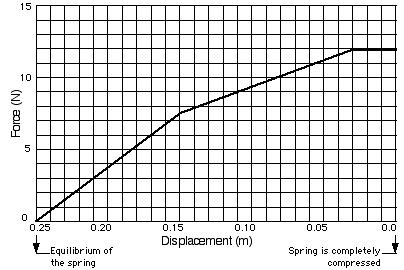
134 How much work is done in compressing the spring all the way back to the handle?
135 If the launcher is held horizontally and the 20.0 gram plane is fired off of it, then with what speed will the plane leave the launcher?
136 What is the spring’s spring constant?
137 If the launcher is held horizontally and the plane is fired off of it, then with what speed will the plane be traveling at 15 centimeters from the equilibrium position?
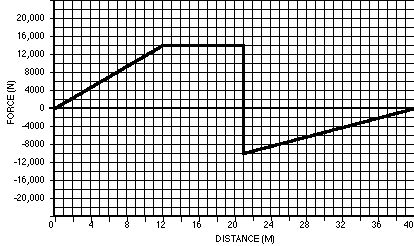
The graph above is a force versus distance graph for a 300 kg Dr.Suess mobile. The reason for the graph’s peculiar nature is due to a wrench left under the hood.
138. How much work is done between 0 and 16 meters?
139. How much work is done between 16 and 40 meters?
140. How much work is done between 12 and 21 meters?
141. How much work is done between 5 and 12 meters?
142. How much work is done between 20 and 28 meters?
143. How much work is done between 18 and 32 meters?
144. What is the car’s speed after traveling from 0 to16 meters if it started from rest?
145. What is the car’s speed after traveling from 0 to 21 meters if it started from rest?
146. What is the car’s speed after traveling from 0 to 40 meters if it started from rest?
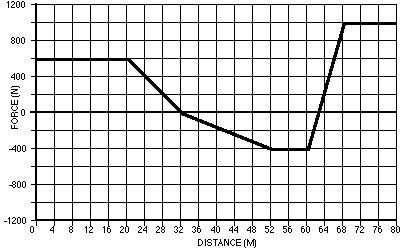
The graph above is for a bicyclist’s ride on level ground. The bicyclist’s mass is 90 kg. The bicyclist starts from rest.
147 What is the work done over the first 12 meters?
148 What is the speed of the bicyclist after traveling 12 m?
149 What is the work done over the first 20 meters?
150 What is the speed of the bicyclist after traveling 20 m?
151 What is the work done over the first 32 meters?
152 What is the speed of the bicyclist after traveling 32 m?
153 What is the work done over the first 52 meters?
154 What is the speed of the bicyclist after traveling 52 m?
155 How much work is done between 32 and 52 meters?
156 Suppose at 52 meters the bicyclist was traveling 5 meters above the ground. How fast would they be traveling?
157 If the bicyclist drops 10.0 meters below the starting height at 52 meters. then how fast would they be traveling?
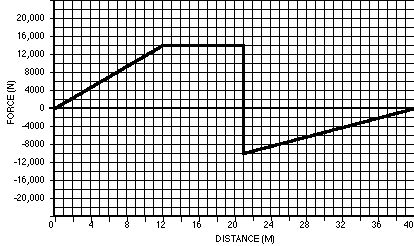
The graph above is a force versus distance graph for a Dr.Suess mobile. The reason for the graph peculiar nature is due to a wrench left under the hood. The vehicle’s mass is 500 kg.
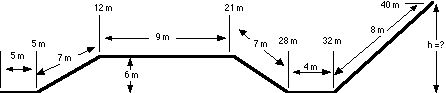
158 How much work is done between 0 and 16 meters?
159 How much work is done between 16 and 40 meters?
160 How much work is done between 12 and 21 meters?
161 How much work is done between 5 and 12 meters?
162 How much work is done between 20 and 28 meters?
163 How much work is done between 18 and 32 meters?
164 What is the speed after traveling from 0 to 16 meters along the diagramed path?
165 What is the speed after traveling from 0 to 21 meters along the diagramed path?
166 What is the speed after traveling from 0 to 32 meters along the diagramed path?
167 What is the maximum height the car will travel to after traveling from 0 to 40 m?
WORK COASTER
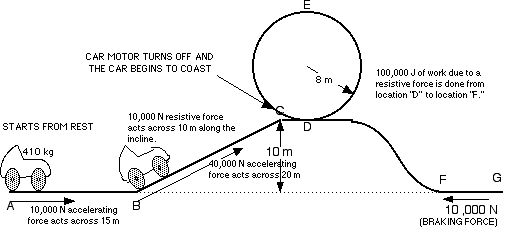
168 How much work is done from location “A” to location “B?”
169 How fast is the car traveling at location “B?”
170 How much work is done from location “B” to “C?”
171 What is the velocity of the car at location “C?”
172 What is the velocity of the car cat at location “D?”
173 How many g’s are felt by the rider at location “D?”
174 How fast is the car traveling at location “E?”
175 How many g’s does the rider feel at location “E?”
176 How fast is the car traveling at location “F?”
177 How much distance is traveled from location “F” to location “G” if the car comes to rest at location “G”
Answers to the “Work Coaster”
168 150,000 J 169 27.05 m/s 170 700,000 J 171 62.85 m/s 172 62.85 m/s 173 51.39 g’s
174 60.30 m/s 175 45.38 g’s 176 60.48 m/s 177 75.00 m
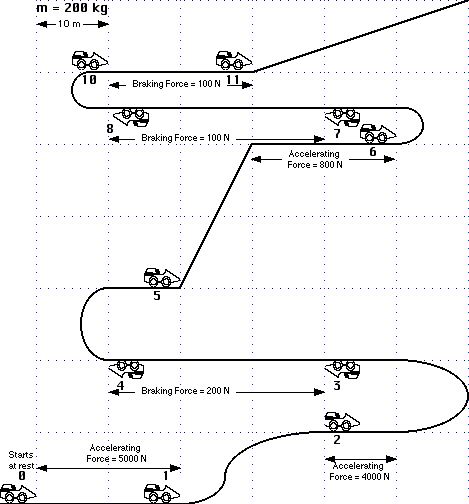
Answer the following based on the coaster shown below.
178 At each number calculate the ET.
179 At each number calculate the car’s velocity.
180 Calculate the acceleration due to each force in m/s2 and g’s.
181 Calculate the acceleration felt by the car as it enters each vertical curve.
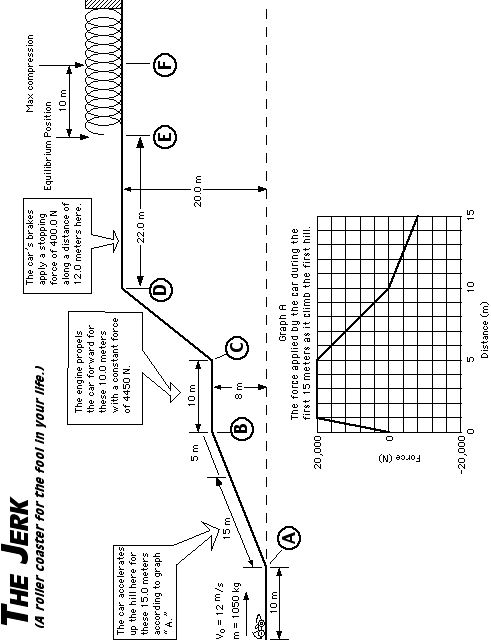
Questions about “THE JERK” roller coaster.
182 What is the velocity of the roller coaster car at location “B?”
183 What is the velocity of the roller coaster car at location “C?”
184 How much power in watts and horsepower are generated by the car as it travels from location “B” to “C.”
185 What is the velocity of the car at location “D?”
186 What amount of power applied to the car to slow it down between location “D” and “E?”
187 What is the spring’s force constant?
189. What is the potential energy of a spring that is compressed 0.53 meters from equilibrium if the spring constant is 219 N/m?
190. What is the spring potential energy of a spring that is stretched 0.23 meters from equilibrium if the spring constant is 12 N/m?
191. What is the spring potential of a spring that is stretched 11.42 centimeters beyond equilibrium if the spring constant is 81 N/m?
192. What is the spring constant of a spring that is stretched 34.2 centimeters if 1298 J of energy is used to stretch the spring?
193. What is the stretched distance of spring with a spring constant of 12.5 N/m if the spring uses 127 J?
194. What is the spring constant of a spring that is stretched 123.2 cm while storing 93 J of energy in the it?

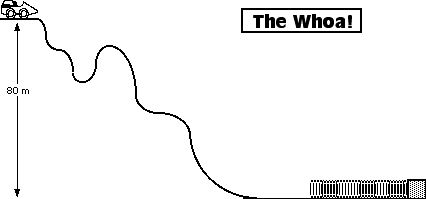
A roller coaster car is to travel from rest down a wavy hill. Then it will coast without friction into the spring. The roller coaster will compress the spring until it comes to rest. The spring constant is 200 N/m. The mass of the roller coaster is 500 kg.
195. What is the total energy of the system at the top of the hill?
196. What is the total energy of the system at the bottom of the hill?
197. What is the total energy of the system before it hits the spring?
198. What Is the total total energy of the system when the spring is completely compressed?
199. What is the speed of the car at a height of 30 m.
200. What is the speed of the car at the bottom of the hill?
201. What is the speed of the car before it hits the spring?
202. What is the maximum distance the spring is compressed?
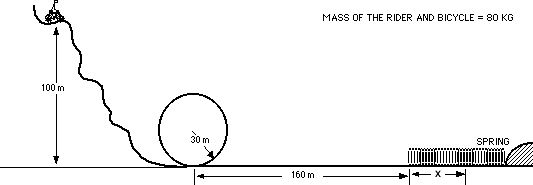
Death-Wish Hershey just finished his design of a new dare devil amusement park ride. The rider coasts down on a special bicycle. The rider starts from rest. This bicycle will not jump off the track. The track is frictionless. The spring constant is 1960 N/m and the mass of the bicyclist and bicycle is 80 kg.
203. How fast is the rider at the bottom of the hill?
204. How fast is the rider traveling half-way up the loop?
205. How fast is the rider traveling at the top of the loop?
206. How fast is the rider traveling at the bottom of the loop?
207. What is the maximum compression distance of the spring?
208. How fast will the rider be traveling when the spring is compressed 1/3 the maximum distance?
209. After the rider bounces off the spring and starts to roll backwards he applies the brakes. He applies the brakes as soon as the spring is back to its equilibrium position. If he is to come to a stop in the 160.0 meters before reaching the loop again, then what average force must be applied by the brakes?
 Below is a ride at Dr. Seuss’s amusement park in “Whoville.” Based on the information diagramed below. Answer the following questions.
Below is a ride at Dr. Seuss’s amusement park in “Whoville.” Based on the information diagramed below. Answer the following questions.
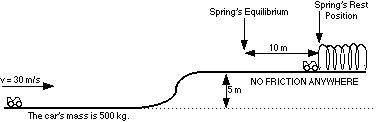
210. What is the speed of the car at the top of the hill?
211. What is the spring’s spring constant?
212. What is the speed of the car when the spring is compressed 5 meters?
213. At which compression distance of the spring is the speed of the car half of what was at the instant it hit the spring?
214. At which compression distance of the spring is the speed of the car half of what it was at the very beginning of the ride?
215. Suppose, by some weird quirk of Seuss’ Science, the spring bounces the car with 3 time the total energy it hit the spring with.
a. What is the velocity of the car when it comes of the spring?
b. What is the new velocity of the car at the very beginning of the ride?

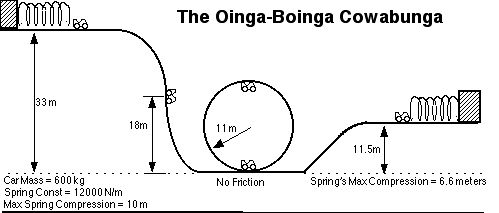
The roller coaster’s car starts from rest.
Convert ALL heights to stories -even the ones given in the questions.
Put ALL speeds in m/s and mph.
Put ALL accelerations in m/s2 and g’s.
Put ALL powers in watts and horsepower.
(NOTE -It takes 0.1 seconds to blink the human eye)
216. What is the speed of the car after it just looses contact with the spring at the top of the first hill?
217. What is the speed of the car when it is 18 meters above the ground?
218. What is the speed of the car as it enters the loop?
219. How many g’s are felt by the rider as the car enters the loop?
220. What is the speed of the car when it reaches the top of the loop?
221. How many g’s are felt by the rider at this point loop?
222. What is the speed of the car as the instant before it makes contact with the spring on the right?
223. What is the spring’s spring constant?
224. What is the speed of the car after the spring has been compressed 4.0 m from equilibrium?
225. What average force did the spring exert to stop the car?
226. How much time did it take to stop the car?
227. How much power was used by the spring to stop the car?
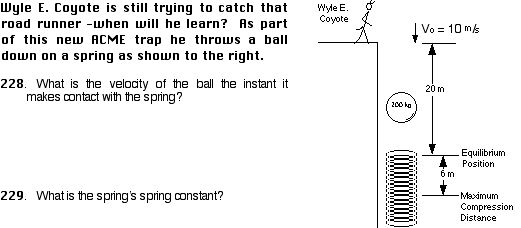
230. How fast is the ball traveling when the spring is compressed 2 meters from the equilibrium position of the spring?
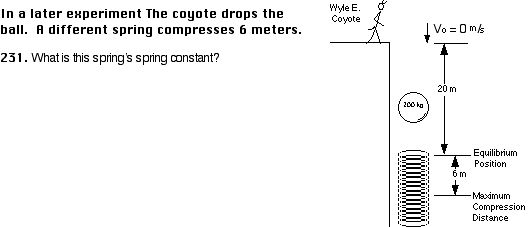
Wile E. Coyote is at it again. This time he is in a rocket boosted glider.
232. The spring is compressed 25 meters. What is the spring’s spring constant if the glider is leave the launch tower at 100 m/s?
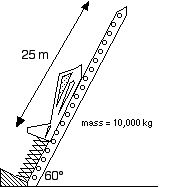
233. The spring is compressed 25 meters. What is the spring’s spring constant if the glider is leave the launch tower at 100 m/s?
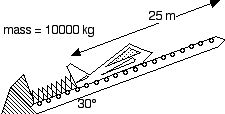
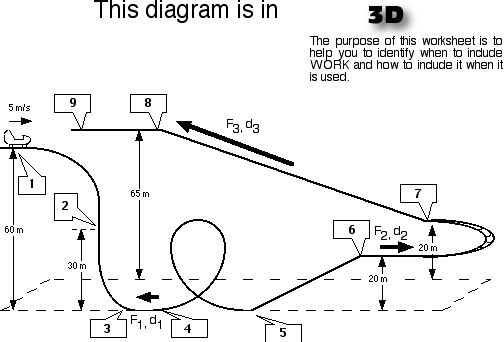
Write the math expression for the total energy relationships between the following locations: (Leave out an energy if its value is zero.)
1 & 2
1 & 3
2 & 4
3 & 5
5 & 6
5 & 7
3 & 7
1 & 9
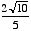 = 1.26
= 1.26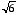
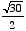 = 2.74
= 2.74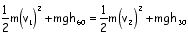
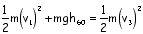
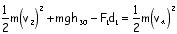
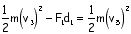
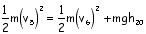
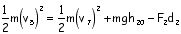
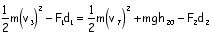
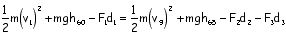

Write the math expression for the total energy relationships between the following locations:
5 & 6 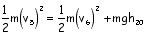
5 & 7 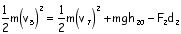
3 & 7 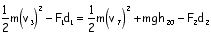
1 & 9 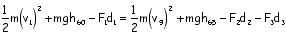
78 15,000 J
79 1,000,000 J
80 6000 J
81 70,000,000 J
82 200 N
83 833.32 N
84 3 m
85 150,000 J
86 15,000 J
87 100 N
88 600 m
89 100 J
90 25,000 J
91 40 N
92 9800 N
93 5196.15 J
94 751754.0 J
95 3109 J
104 20.66 m/s
105 8.94 m/s
106 509.90 m/s
107 124.10 m/s
108 108.65 m/s
109 2,084,870.49 N
110 8.94 m/s
111 68.65 m/s
112 69.95 m/s
113 (a) 1,000,000 J (b) 267261.24 w,? hp
114 (a) 2940 J (b) 98 w, 0.131 hp
115 (a) 652,548 J (b) 99,676.71 w, 133.61 hp
116 (a) 652,548 J (b)73,500 w, 98.53 hp
117 (a) 3,000,000 J (b) 981,980.51 w: (t=3.06 sec)
118 (a) 490 J (b)57,166.67 w: (t=1.00857 s)
119 (a) 8 J (b) 46.19 w: (t=0.17 s)
120 720 J
121 1400 J
122 1560 J
123 1160 J
124 - 400 J
125 0.21 J
126 0.63 J
127 0.93 J
128 9.65 m/s
129 9.23 m/s
130 17.45 m/s
131 w = 128,571-53571.5+25,000 = 99,999.5 J: v = 13.48 m/s
132 w = 599,999.5 J: v = 31.51 m/s
133 29.92 m/s
134 w from 0 tp 0.03 = 0.354: w from 0.03 to 0.15 = 1.158: w from 0.15 to 0.25 = 0.375 Therfore work = 1.887 J
189. 30.76 J
190 0.317 J
191 0.528 J
192 22.194 J
193 4.51 m
194 122.54 N/m
195 392,000 J
210. 28.32 m/s
211. 4010 N/m
212. 24.53 m/s
213. 8.66 m @ 14.16 m/s
214. 8.48 m
215. a. 51.00 m/s
b. 51.96 m/s
216. 44.72 m/s
217. 47.90m/s
218. 51.45 m/s
219. 25.55 g’s felt
231. 2831.11 N/m
232. 166,789.64 N/m
233. 163,920 N/m
189. 30.76 J
190 0.317 J
191 0.528 J
192 22.194 J
193 4.51 m
194 122.54 N/m
195 392,000 J
8 ???
9. ???
10. ???
11. 31.30 m/s2
12. 39.60 m/s
13. 39.60 m/s
14. 62.61 m
15. 44.27 m/s
16. 37.04 m/s
17. 28 m/s
18. 44.27 m/s
19. 8.94 m
20. 41.74 m/s @ 2.98 m
21. 490 N
22. 28.32 m/s
23. 4010 N/m
ANSWERS
24. 24.53 m/s
25. 8.66 m @ 14.16 m/s
26. 8.48 m
27. a. 51.00 m/s
b. 51.96 m/s
28. 44.72 m/s
29. 47.90m/s
30. 51.45 m/s
31. 25.55 g’d felt
32. 47.07 m/s
33. 19.55 g’s felt
34. 49.21 m/s
35. 33,352.62 N/m
36. 39.16 m/s
37. 223,156.362 N
38. 0.13 s
39. 660,095.70 w, 884.85 hp
40. 22.18 m/s
41. 3386.67 N/m
42. 21.53 m/s
231. 2831.11 N/m
232. 166,789.64 N/m
233. 163,920 N/m
Other sheet

- # - Another fine worksheet by T. Wayne
by Tony Wayne ...(If you are a teacher, please feel free to use these resources in your teaching.)
The owner of this website does not collect cookies when the site is visited. However, this site uses and or embeds Adobe, Apple, GoDaddy, Google, and YouTube products. These companies collect cookies when their producs are used on my pages. Click here to go to them to find out more about how they use their cookies. If you do not agree with any of their policies then leave this site now.