Loops
(Circular Motion,
Potential Energy
and Kinetic Energy)
Coaster Design Home Page
LOOPS
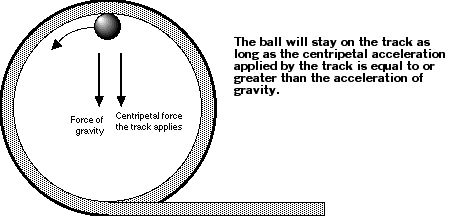
CENTRIPETAL FORCE
The average person on the street has heard of centrifugal force. When asked, they would describe this force as the one pushing an object to the outside of a circle. There is only one problem with this description. There is NO FORCE pushing an object to the outside.

For a person riding in a car while traveling in a circle, he perceives a force pushing him to the outside of the circle. But what force is physically pushing him? It can not be friction. Frictional forces oppose the direction of motion. It can’t be a “normal force1 .” There is not a surface pushing the rider to the outside. To travel in a circle, a force pointing to the inside of the circle, or curve, is needed. The force pointing to the inside is called the centripetal force.

To understand a source for the misconception of the direction of this force, consider what it feels like when traveling around a corner in the back seat of a car. Everyone who has been in this situation knows that the passenger will slide to the outside of the curve. To understand that there is no force pushing the passenger to the outside, a change of reference frame is needed. Move the point of view from inside the car to a location outside, above, the car.
A COASTER’S LOOP
On a well designed roller coaster loop, the riders will not be able to sense when they are traveling upside down. This is done by making sure the force that is exerted on the rider is at least equal to the weight of the rider.
Centripetal force applied to the track depends on the velocity of the car and inversely to the radius. The formula is:
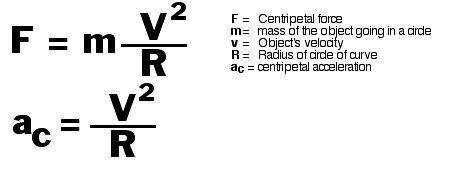
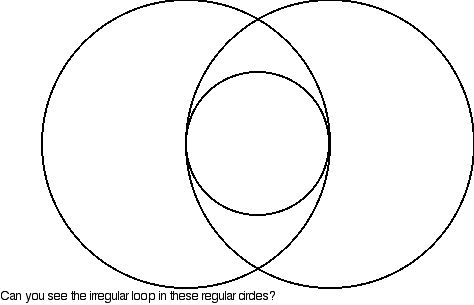
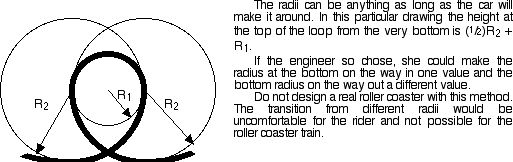
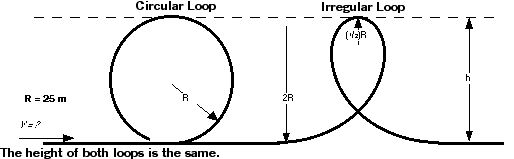
In order to apply enough centripetal acceleration the roller coaster car has to either be traveling very fast or the radius of the loop has to be made small. Most rides have a tall loop. A tall loop means a big radius. The problem is, as a car goes up, it slows down. The higher it goes, the slower it will be traveling over the top. In order to apply a centripetal force equal to gravity, 1 g, at the top, the car must be traveling extremely fast as the rider enters the loop. On some of the early round loops, the riders actually had their necks broken as a combination of the sudden rise in the loop as they entered at an extremely high rate of speed. As a compromise, the loops today are designed around an irregular shape called a klothoid or spiral of Archimedes. These irregular loops allow a circular figure whose radius changes.

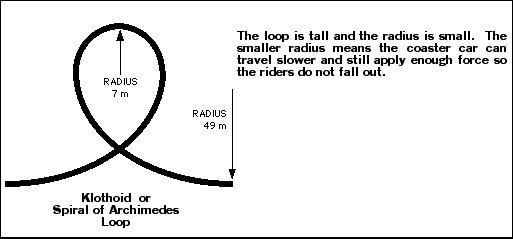
For the advanced reader, the formula for the klothoid shape is:
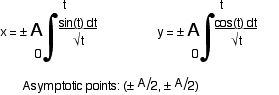
The formula for the “Spiral of Archimedes” in polar form is
r = aq
where “a” describes the magnitude of the spiral and “q” is the angle through which the spiral is formed. To make a loop, the spiral will have to be mirrored horizontally.
Nothing is perfect in engineering. These designs operate under ideal circumstances. In real life, the curves need to be tweaked into the right shape.
The Simple Irregular Loop
Sometimes it is not necessary to go into all the math to have a little fun with the irregular loop. These loops can be simulated using the combination of semi-circles of different radii.
Other loop possibilities

Physiological
Effects of
Acceleration
(Acceleration,
Circular Motion,
Kinetic Energy,
and Potential Energy)
BACKGROUND
Imagine a passenger riding through a loop on a roller coaster. The passenger’s head is towards the inside of the circle.
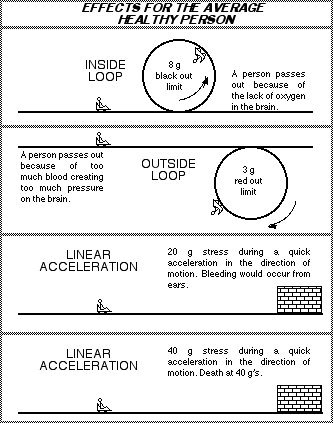
Her feet are to the outside of the circle. In order to keep blood in the passenger’s head, a centripetal force needs to be applied to the blood to push it upwards toward the head and the center of the circle. The heart applies the centripetal force on the blood. A passenger can experience many g’s in a loop. Recall that a g is the number of times heavier an object becomes. A 7 g experience means that the passenger feels 7 times heavier. Everything about the passenger becomes 7 times heavier. Her 3 pound brain now weighs 21 pounds. Every ounce of blood becomes 7 times heavier. If the blood feels too heavy the heart cannot apply enough force to push it towards the head. If the brain does not get any blood it will not get the oxygen the blood carries. The passenger will pass out within a second.
THE EXTREME EXPERIENCE
You are riding a new untested roller coaster when something goes wrong. As you enter the first big loop, a great pressure pushes you down. You slouch down in the seat from the extra weight. Over the top of the loop the roller coaster car slows down. The extra weight on your legs, lap, and shoulder make it impossible to sense that you are upside down. Out of the loop, over a hill and into another loop. This loop has a smaller radius. The car is traveling much faster now. As the g forces climb up toward 7 g’s, you sink further still in the seat. You can no longer see color. Everything appears in black and white. An instant later, the passenger next to you disappears from view. Your field of vision is shrinking. It now looks like you are seeing things through a pipe. The front corner of the car disappears from view as your peripheral vision disappears. The visual pipe’s diameter is getting smaller and smaller. You sink into the seat further still as the number of g’s climb further. In a flash you see black. You have just “blacked out.” You are unconscious until the number of g’s are reduced and the blood returns to your brain.
Amusement park owners and insurance companies don’t want the previously described situation to occur. It would limit repeat riders and the number of potential consumers who can safely ride the coaster. Most roller coasters keep the g’s felt under 5 g’s on an inside loop or the bottom of a dip after a hill. When a rider travels over a hill at a high rate of speed, he experiences negative g’s. A negative g is the multiple of a person’s weight that is needed to keep a rider in his seat. Negative g’s also force the coaster car to try to come up off the track. Negative g’s are a rider’s heaven and a designer’s nightmare. Negative g’s are avoided as much as possible.
A negative g has a different effect on a rider than a positive g. Both negative and positive g’s can cause a rider to pass out. But negative g’s cause a rider to “red out.” A red out condition occurs when there is too much pressure on the brain caused by too much blood in the head. The extra pressure can cause blood vessels to burst and kill the rider. This is a sure way to limit the number of repeat riders.
There is another way for a rider to experience negative g’s. It is related to the length of the train. The roller coaster track is designed for the dynamics at the center of mass of the coaster train. Negative g’s are experienced by the rider at the back of the train as he travels over a hill. For an empty train, the center of mass is in the middle of the train.Whatever speed is acquired by the center of the train is the speed for the entire train. After the center of a train passes over a hill it begins to gain velocity. As the center speeds up so does the back of the train. This means that the rear of the train will travel over the hill faster than the middle of the train. If the rider travels over the hill faster than the designed velocity of the hill the rear car will be whipped over the hill.
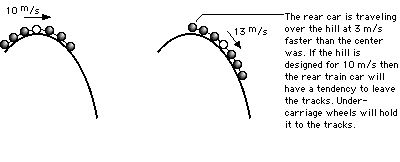
SOME “g” DETERMINATORS:
CALCULATION OF THE G’S FELT
To calculate the g’s felt, a formula from circular motion will be utilized. Since energy relationships do not utilize time, the circular motion formula used will also not utilize time.


Where “v” is the velocity of the body and “R” is the radius of the circle traveled. To calculate the velocity a body is traveling, use energy relationships to solve for the kinetic energy and the associated velocity. One more thing. To calculate the g’s felt remember that the g’s felt by the rider is the normal force on the seat of the rider divided by the mass then converted into g’s. As a rider enters a loop he will feel 2 forces.
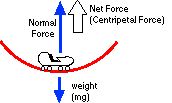
The real number of interest is the number if g’s felt by the passenger traveling in the vertical circle. The g’s felt are calculated below.
SFy = m(ac) = (Normal Force) - Weight
SFy = mv2/R = (Normal Force) - mg
\ (Normal Force) = mv2/R + mg
recall that... (Normal Force)/mg = g’s felt by the rider
thus... (Normal Force)/g = mv2/R/mg + mg/mg
\ g’s felt by the rider = (centripetal acceleration in g’s) + 1 at the bottom
These results can be summarized as follows...
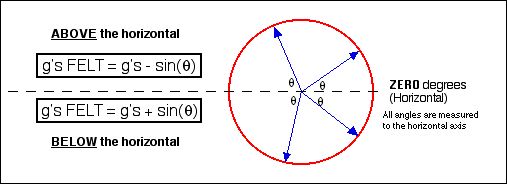
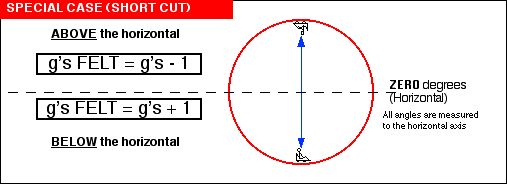
These results can be interpreted easily. As a rider enters the loop, the track has to exert a normal force upwards to supply the necessary centripetal force and acceleration to make the rider travel in a circle. But because the loop is vertical and the rider is at the bottom the normal force not only has to supply the centripetal force but must also overcome the pull of gravity. That’s why 1 g is added in the equation. At the top of the loop, 1 g is subtracted from what is felt because the pull of gravity is helping the normal force exerted by the track instead of needing to be overcome.
EXAMPLE 1

SOLUTION
To calculate the g’s at the top of the loop, you will need to know the velocity of the rider there. To find velocity, use kinetic energy.
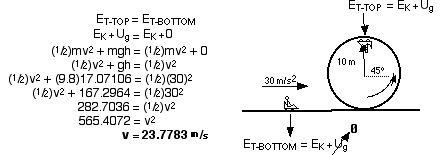
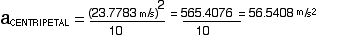
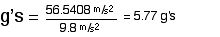
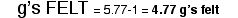
The rider will not pass out because 4.77 is less than 8 g’s.
EXAMPLE 2

SOLUTION

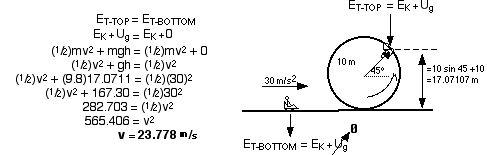
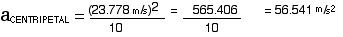
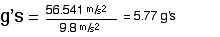
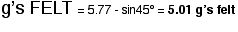
The rider will not pass out because 5.01 is less than 8 g’s.
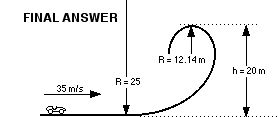
THE IRREGULAR LOOP EXAMPLE
The simple loop is easy enough to calculate. The irregular shaped loop needs a little more work. The velocity as the car enters the loop should be known. First establish the g’s felt at the bottom. Subtract one g to know what the track exerts. Then convert these g’s to m/s2. Now solve for the radius.
EXAMPLE
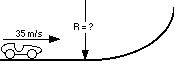
STEP 1 (I’m randomly choosing 6 g’s as the limit for the rider)
Therefore the centripetal acceleration of the track is 6g - 1g = 5g’s.
STEP 2 (convert these g’s to m/s2)
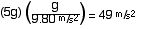
STEP 3
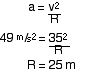
Now to calculate what the rider feels at the top of the loop.
Decide on the height of the loop. Then decide how many g’s the rider will experience. Use the loop formulae with centripetal acceleration to calculate the radius.
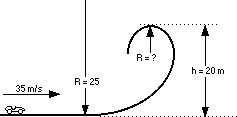
STEP 4
The top of the loop will be at 25 m. (Chosen pretty much at random.)
STEP 5
I’m randomly choosing 6 g’s again as the limit for the rider. It could be almost any number. At the top of the loop add 1 g for the centripetal force. (“Add” because the rider is upside down.)
6g’s + 1 g = 7g
STEP 6 convert g’ to m/s2
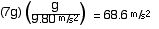
STEP 7
(1/2)(m)(35)2 = (1/2)(m)vo2 +(m)(9.80 m/s2)(20 m)
The m’s divide out.
(1/2)(35)2 = (1/2)vo2 +(9.80 m/s2)(20 m)
vo = 28.86 m/s
STEP 8
Calculate the radius at the top
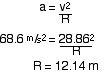

In reality, a person will not pass out the instant he/she reaches 8 g’s. It will take a few seconds of being at 8 g’s for the person to pass out. But for the sake of easy calculations we will assume that the instant 8 g’s is reached a person will pass out. 8 g’s is an average. peaple generally pasout between 6 to 10 g’s. (FYI: The 40 g mark mentioned earlier is instantaneous for death.)
1 What must the velocity of the car be at the top of the circular loop such that the rider FEELS weightless at the top of the first loop?
2 What must the velocity of the car be at the bottom of the circular loop such that the rider FEELS weightless at the top of the first loop?
3 How many g’s does the rider feel as he enters the circular loop, at the bottom?
4 How fast is the rider traveling when he enters the irregular loop?
5 How many g’s does the rider feel as he enters the irregular loop?
6 How fast is the rider traveling at the top of the irregular loop?
7 How many g’s does the rider feel at the top of the irregular loop?
NEW SET OF PROBLEMS
8 How fast must the car be traveling at the top of the klothoid loop if the rider is to experience 2.00 g’s?
9 How fast would the rider be traveling as she enters the irregular loop?
10 How many g’s does the rider feel as she enters the irregular loop?
11 How many g’s does the rider feel as she enters the circular loop?
12 How many g’s does the rider feel as she passes over the top of the circular loop?
ANSWERS
1 15.65 m/s 2 35.00 m/s 3 6 g’s 4 35 m/s
5 3.5 g’s 6 16.65 m/s 7 1.00 g’s 8 19.17 m/s
9 36.71 m/s 10 3.75 g’s felt 11 6.50 g’s felt
12 0.50 g’s (He feels like he might fall out of his seat.)
|