|
|
| This text is meant to accompany class discussions. It is not everything there is to know about uniform circular motion. It is meant as a prep for class. More detailed notes and examples are given in the class notes, presentations, and demonstrations (click here.) |
| |
| Introduction |
"Uniform circular motion" means that a body is turning or traveling at a constant speed. It is not speeding up or slowing down. See the animation below for a comparison of the the two types of circular motions.
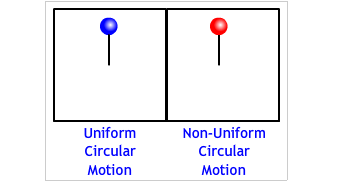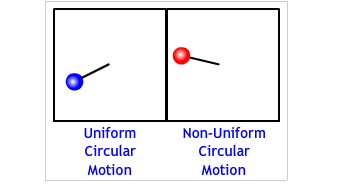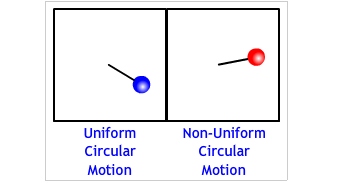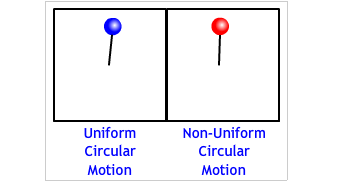
Usually, when we think of a car accelerating, we think the car as traveling in a straight line and its speed is changing, i.e. speeding up or slowing down. The motions we have calculated has been one dimensional (along a line.) Up to now an acceleration has meant a change in the velocity's MAGNITUDE with no change in direction.
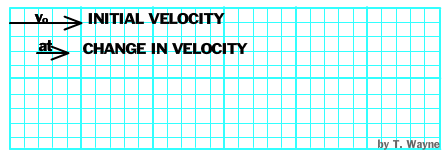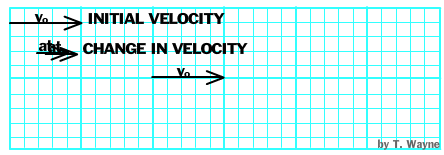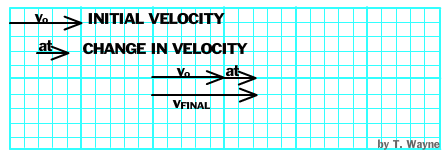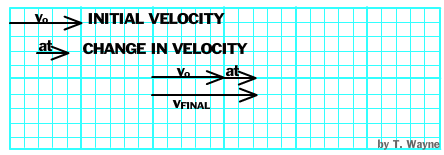
Notice how "at" is in the same direction as the velocity. This also shows that a force in the same direction as the velocity will change the body's speed and any direction change would occur along the same straight line. But what would happen if the force was NOT applied parallel to the direction of the motion?

A force that is not applied parallel to the velocity changes the body's direction. (As in the animation above.) It may or may not change the velocity's magnitude. |
You can see from the animation that to change the direction of a moving body, a force is applied at an angle to the motion. This is a change in the velocity's direction and is therefore an acceleration.
Recall that position, velocity, acceleration and force are all vectors. This means that each has direction and magnitude. If you change a velocity's direction OR magnitude then you have created an acceleration. In circular motion we are going to look at position, velocity, acceleration and force. We will look at defining the direction and then the magnitude.
|
| Direction |
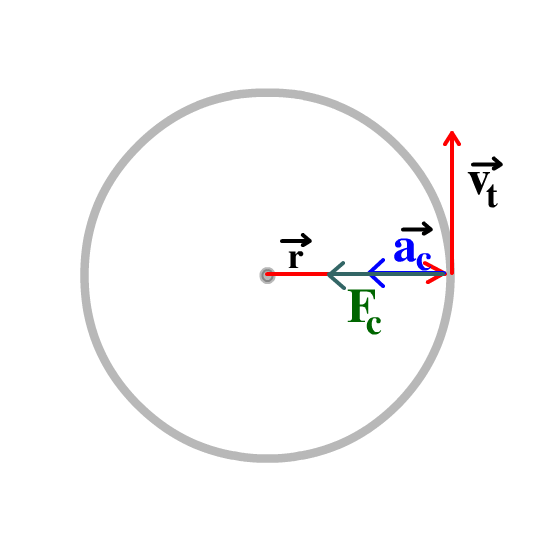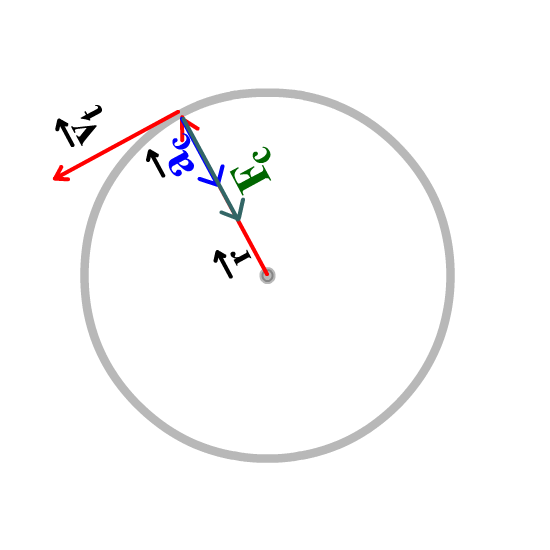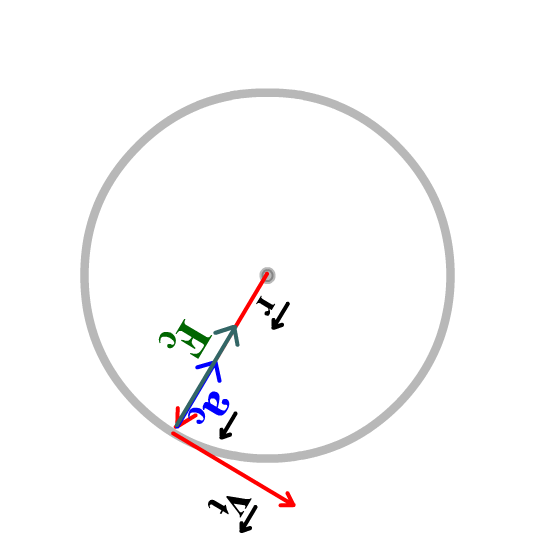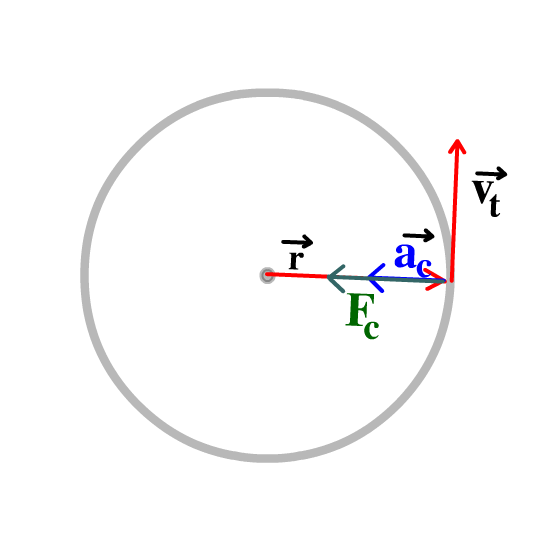
The radius is the position or radius vector starts at the center and points to the body's location. (See the animation below.)
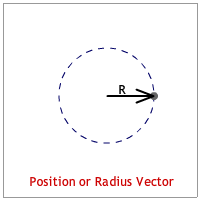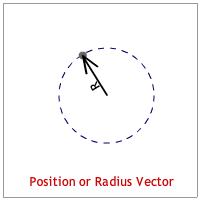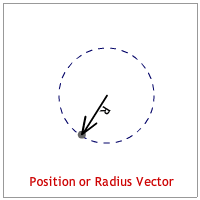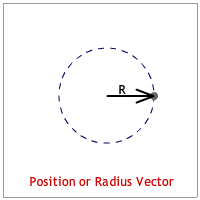
The velocity vector is tangent to the circle and is identified as the "tangential velocity." This makes it perpendicular to the radius vector. (See the animation below.)
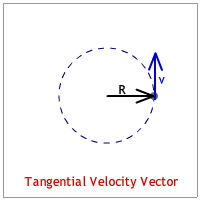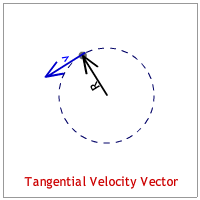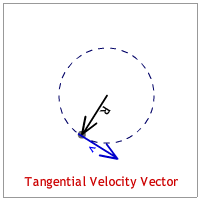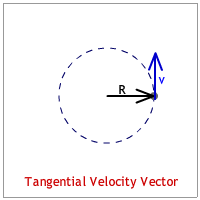
The acceleration vector points to the center of the circle. Since it seeks the center of the circle it is identified as the "centripetal acceleration."(See the animation below.) [Any quantity pointing to the center of the circle is described with the adjective, "centripetal."]
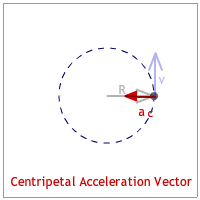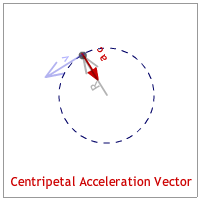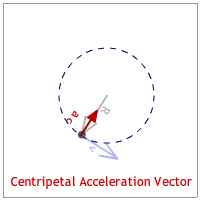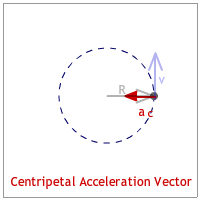
The centripetal force is the force that also points to the center of the circle. It can be a vector that is drawn shorter, equal, or longer than the centripetal acceleration vector. (See the animation below.)
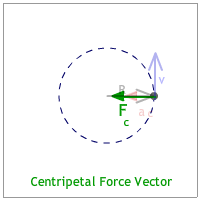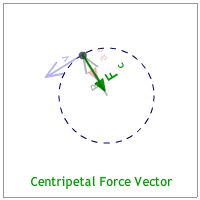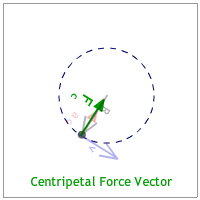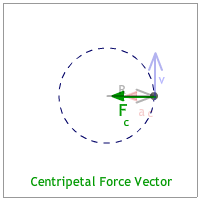
When all the vectors are combined it looks like the animation below. |
 |
| Magnitude |
Time is a special measurement for circular motion. Because the motion repeats itself, the time comes in groups. For example, a Ferris wheel spins once every 1/2 minute, (30 seconds.) If the Ferris wheel spins for 5 minutes, then Ferris wheel has spun 10 times or in 10 groups of 30 seconds. Each time-group is called a "period." A period of motion is the time to get back to the stating position. The repeating motion is called a "cycle." Therefore a period is defined as the time to complete one cycle of motion. Use a capital "T" to represent the period in math equations . [A lower case "t" is a generic variable for any amount of time. It is the wrong variable if you mean the period.]
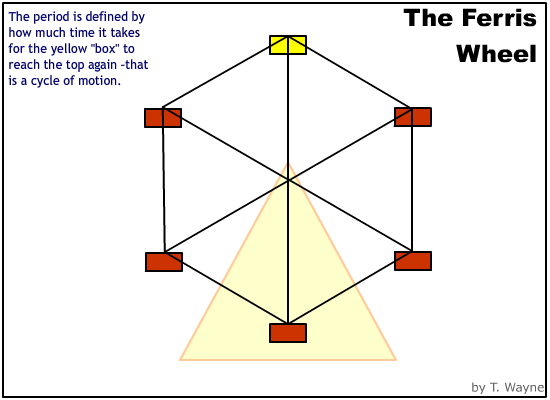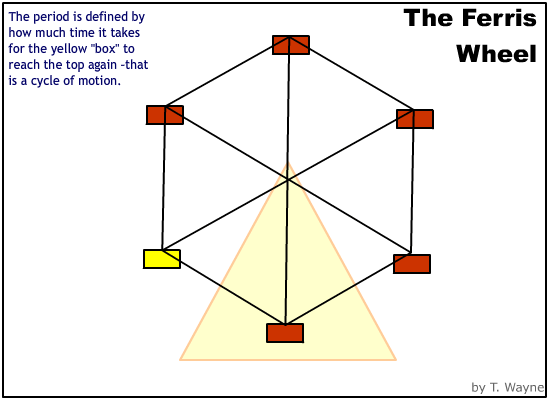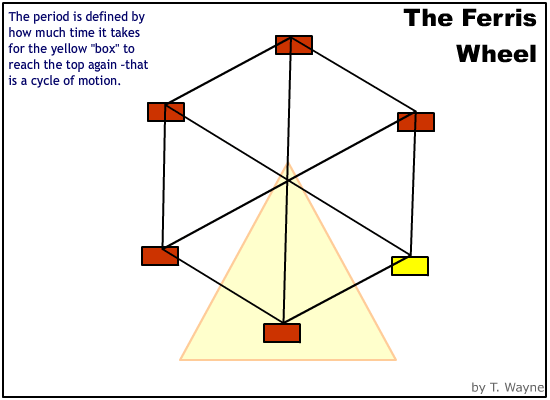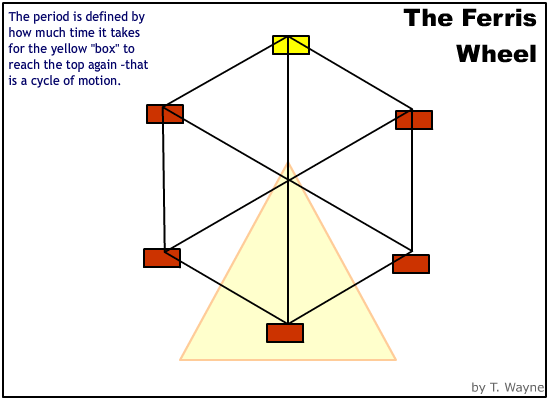
Another term used to describe the relationship between time and the cycles is the frequency. The frequency is the defined as the number of cycles per second. Use a lower case "f" in the equations to represent frequency. [An upper case "F" stands for force, NOT frequency.]

If the Ferris wheel spins with a period of 30 seconds then it will spin with a frequency of (1/30)Hz. |
| More math formulas and examples are in the notes. |
| Period and frequency |
The period describes the time to complete a cycle of motion. It is measured in
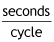
However, a cycle is not a unit, so the period is just measured in the S.I. unit of seconds. It is calculated bu taking the time to complete a number of cycles and dividing it by the number of cycles.
Frequency is the inverse of period. It is described as
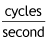
"Cycles" do not have a unit of measurement. Because it is "unit-less" the the number one replaces the unit in the unit's fraction for frequency. This means that frequency is measured in units of
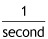
However, the standard unit of second-1 is named after Franc Hertz and instead is called a "Hertz." Abbreviated as "Hz."
| Example 1 |
What is the period of merry-go-round that spins around 3 times in 90 seconds?
| Strategy: |
"3 times" is the number of cycles. 90 seconds is NOT the time to go around once. It is the time to complete the task. This information is used to calculate the period, "T," from the definition of period. Period is the time divided by the number of cycles. |
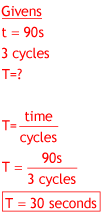
|
|
| |
| Example 2 |
In addition to a speedometer, some cars have a "tachometer." The tachometer reports how fast the engine camshaft is spinning. The tachometer tells the drive this rotation speed in revolutions per minute, abbreviated as "RPM." typically and idling car's engine will experience 600 RPM. That is |
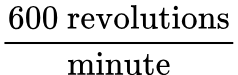 |
What is the period, in seconds, of the rotating engine shaft?
What is the frequency, in Hz, of the rotating engine shaft?
|
In addition to a speedometer, some cars have a "tachometer." The tachometer reports how fast the engine camshaft is spinning. The tachometer tells the drive this rotation speed in revolutions per minute, abbreviated as "RPM." typically and idling car's engine will experience 600 RPM. That is |
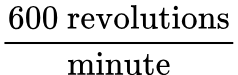
|
(a) What is the period, in seconds, of the rotating engine shaft?
(b) What is the frequency, in Hz, of the rotating engine shaft? |
| Solution |
 |
|
| |
| |
|
| |
|
|