 |
 |
Page 7  |
|
|
| Loop Design and Anaylsis |
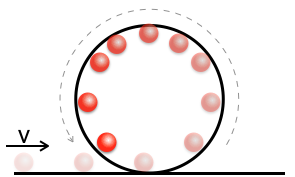 |
| Here is a ball traveling around a vertical loop. What are some of the things we can analyze for this motion that relates to circular motion. To begin with look at the free body diagram of all the force acting on the ball as it enters the loop. |
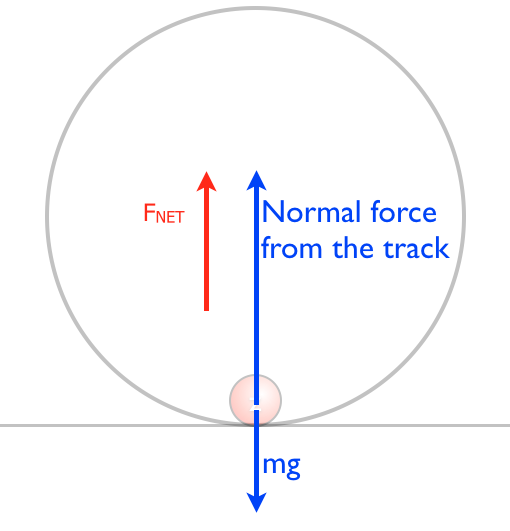 |
| In this situation, the net force is the centripetal force. the normal force, exerted by the track, is the force felt by the rider -that the ball in this model. So not the free body diagram looks like this. |
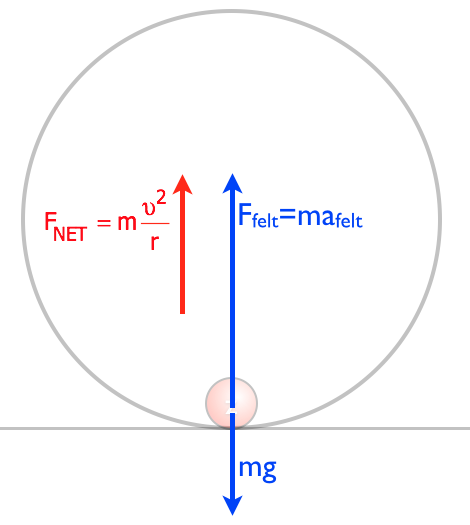 |
| With this free body diagram we can start to sum up the forces in the y-direction. |
 |
| This analysis holds for the top and bottom of any curved motion. It does need to part of an actual loop. -Like in the pictures below. |
 |
| How to interpret this information |
A "g" is a force factor. 1 g is experienced by standing on the surface of the Earth. If you were to stand on a ssale the reading would be what you would expect. If you were to experience 2 positive g's while standing on a scale, then its reading would double. Your bood weighs twice as much and each body part would also double in weight. This makes it more challenging to lift your arm.
For the typical rider, at around 3-6g's, they could experience seeing everything in black and white and given enough time or higher g's, the rider would begin to see stars. This is because the weight increase of the blood becomes more dificult for the heart to pump up to the head. The blood pressure in the rider's head is reduced. The delivery of oxygen to the head is reduced. If this continues for an exened period of time it is probable that the typical rider will passout. These bench marks vary from rider to rider depending on the heart's strength.
g's can be negative and positive. Positive g's occur when the change in velocity is in the direction of a person's head. Negaitve g's occur when the change in velocity is in the direction of the person's feet. |
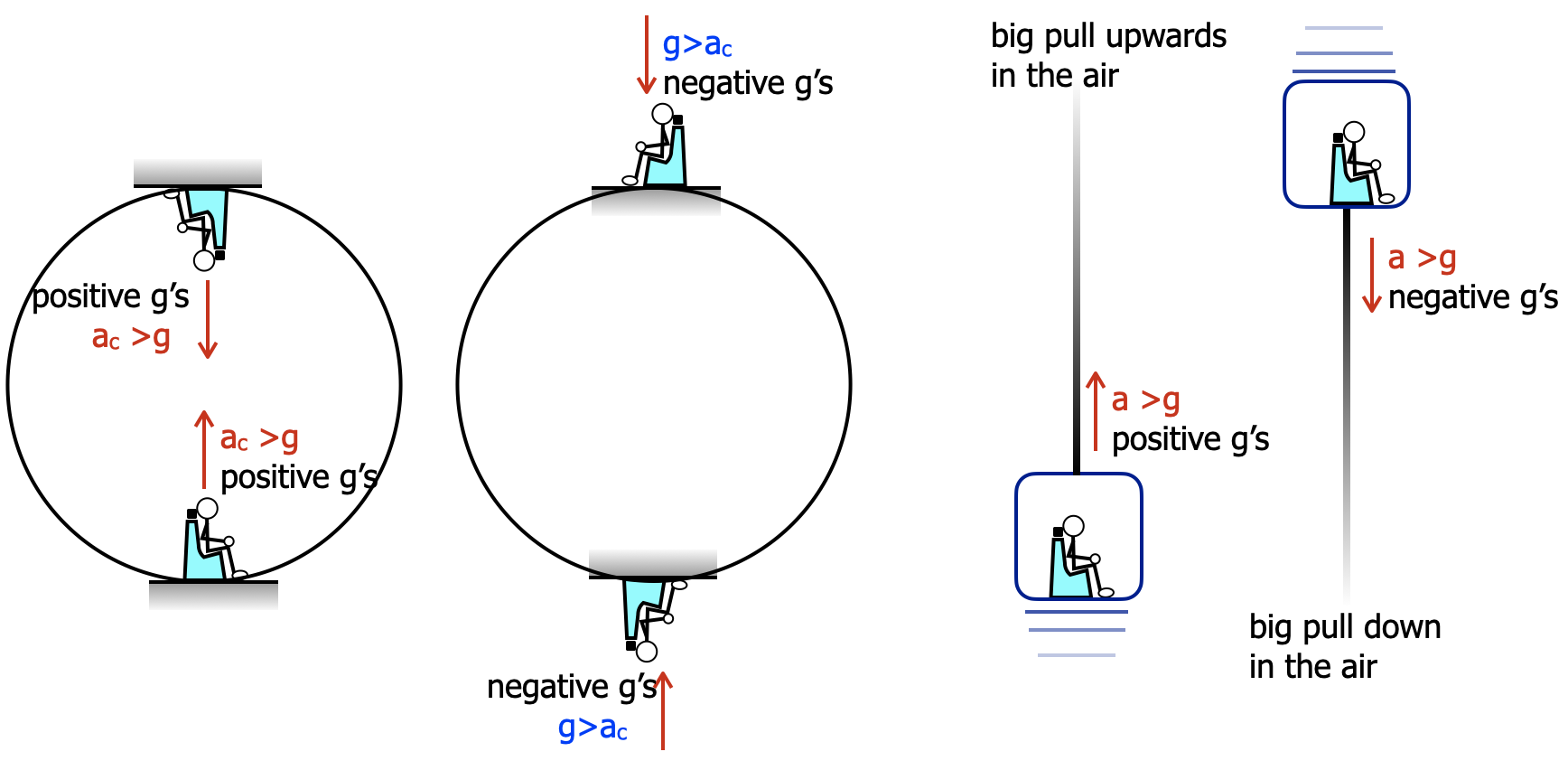 |
When experiencing positive g's greater than gravity's acceleration, the harness does not hold a rider in the seat. When experiencing negative g's, the harness is needed to keep the rider in the seat. Amusement park rides are made to have a no or very little nagative g's. Negative g's are much more dangerous. They lead to an increase in pressure in the head and could possibly result in brain anurisms and death at g's as small as 2 g's or less.
On a roller coaster loop the g's at the bottom need to be small enough so the rider does not pass out. A the top of the loop when the rider is upside down, the centripetal acceleration needs to greater than the acceleration of gravity to keep the rider in the seat but less the the the limit causing the rider to pass out. Most "thrilling" roller coasers will keep the positive g's to less then 5 on loops when entering the loop and greater than 2 when the rider is upside down. |
| |
| |
| Example |
| A rider on a roller coaster is traveling at 225 m/s while at curved roller coaster hill. The hill has a radius of 10 m/s. How many g's does the rider feel? |
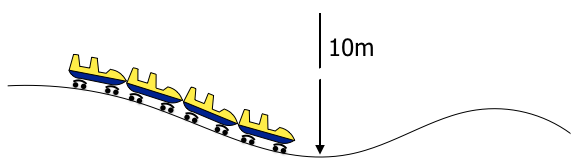 |
Solution

|
|
| |
| Example |
Below is a large circular loop.
(a) How many g's are felt by a driver at the top of the loop if the car coasted around the loop?
(b) Calculate the velocity of the car at the bottom of the loop assuming no friction and it coasted the whole time.
(c) How many g's are felt by the driver as she enters the loop at the bottom? |
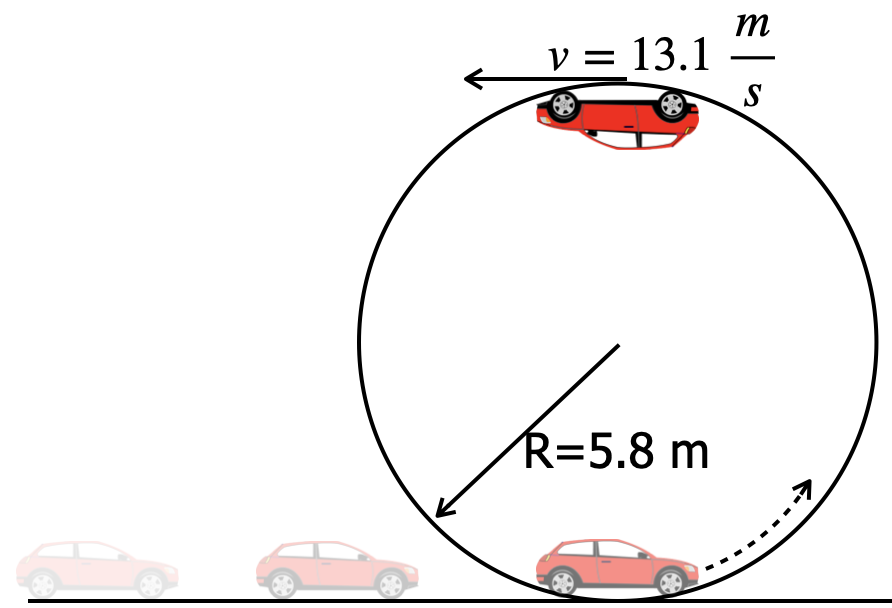 |
| Hints |
Below is a large circular loop.
(a) How many g's are felt by a driver at the top of the loop if the car coasted around the loop?
(b) Calculate the velocity of the car at the bottom of the loop assuming no friction and it coasted the whole time.
(c) How many g's are felt by the driver as she enters the loop at the bottom? |
 |
(a)
Use ac=v2/R to calculate the centripetal acceleration? Convert this to g's. Subtract 1 g to account for gravity pointing in the same dirction as the centripetal acceleration. |
(b)
Use conservation of energy repationships to calculate the velocity a the bottom. The height beween the bottom and the top of the loop is 2R. |
(c)
Use ac=v2/R to calculate the centripetal acceleration? Convert this to g's. Add 1 g to account for gravity pointing in the opposite dirction of the centripetal acceleration. |
|
|
| |
|