|
|
| This text is meant to accompany class discussions. It is not everything there is to know about uniform circular motion. It is meant as a prep for class. More detailed notes and examples are given in the class notes, presentations, and demonstrations. See the links below. |
|
Conservation of Mass-Energy
(The Mass Defect) |
An atom with one proton is called Hydrogen. One proton and 2 neutrons is called "tritium." Its symbol is 3H. It mass is 5.00827 × 10-27kg. The mass of a proton is 1.6727 x 10-27kg. The mass of neutron is 1.6750 x 10-27 kg. The mass of tritium does not equal the sum of its particles. |
| 1 proton |
(1)1.6727 x 10-27kg |
| 2 neutrons |
(2)1.6727 x 10-27kg = 3.3454 x 10-27kg |
| sum |
5.0181 x 10-27kg |
|
The individual parts mass more than tritium atom by 0.0098 x 10-27 kg. Logic says these should match. It take energy to bind these three particle together to create a tritium atom. In fact it take an amount of energy equal to the mass difference. This difference is refereed to as the "mass defect." The mass defect is the binding energy.
Use E=mc2 to calculate the binding energy. In this case.
E = mc2
E = (0.0098 x 10-27 kg)(3.00x 108m/s)2
E = 8.85 x 10-13 Joules |
This means it takes 8.85 x 10-13 Joules to hold this nucleus together. The binding energy of tritium is 8.85 x 10-13 J
|
| Half Life |
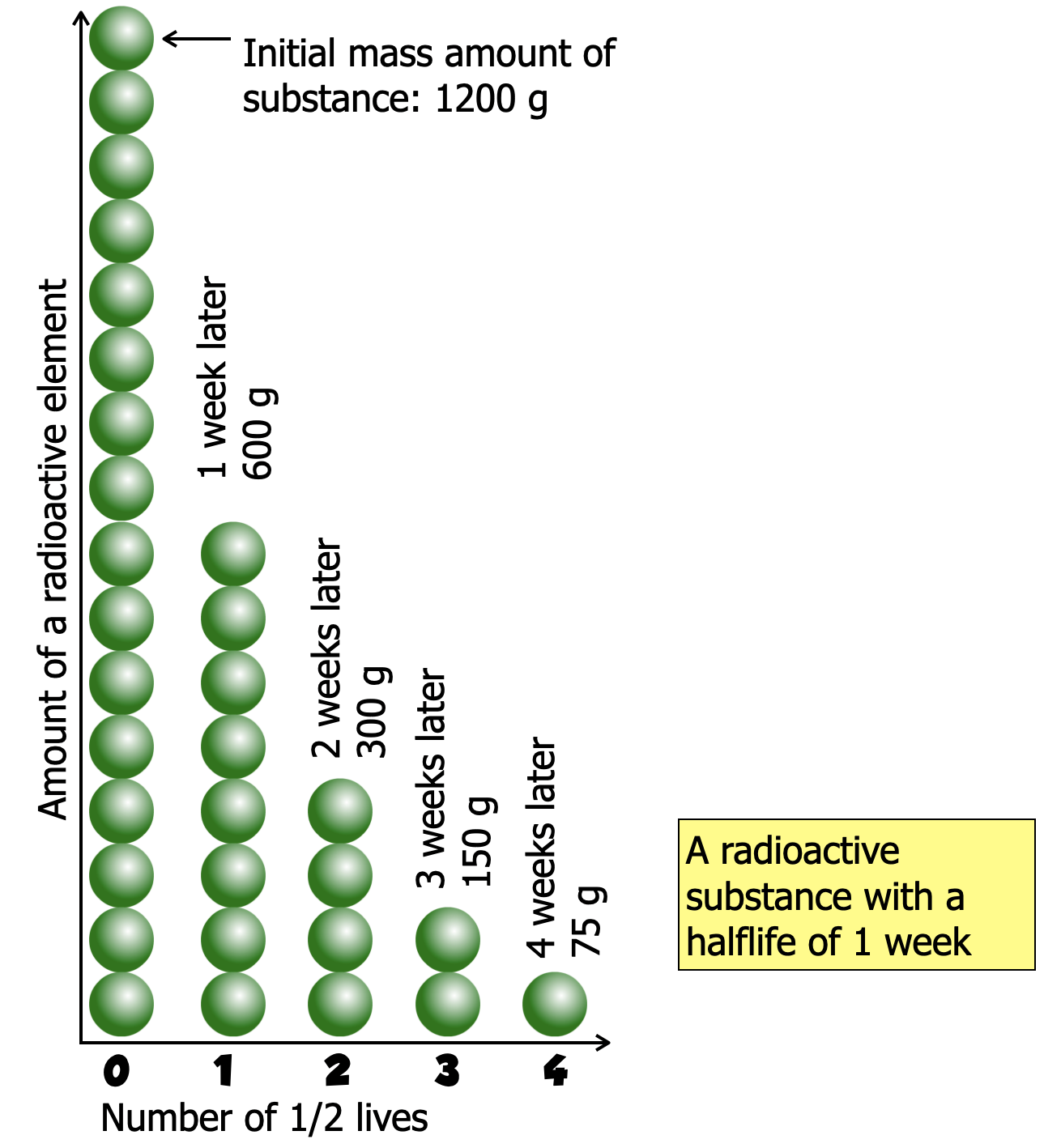
The half life is the time for the 1/2 of the element's nuclei to transmogrify into another isotope/element.
This graph shows how the amount of the radioactive element changes over time. The horizontal axis is showing the number of half-lives. Each half life shows half of the previous amount of a substance's nuclei. |
Exactly 1200 grams of 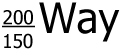 sits in a sealed container. sits in a sealed container. 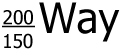 has a half-life of 1 week. how much has a half-life of 1 week. how much 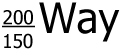 remains after 4 weeks? remains after 4 weeks?
Start week zero with the initial amount of a substance. Then divide the previous amount by half each week until you get to 4 weeks. |
| Half Lives |
Time |
Amount |
| 0 |
0 |
1200 g |
| |
|
|
| |
|
|
| |
|
|
Exactly 1200 grams of 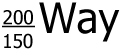 sits in a sealed container. sits in a sealed container. 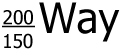 has a half-life of 1 week. how much has a half-life of 1 week. how much 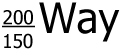 remains after 4 weeks? remains after 4 weeks?
Start week zero with the initial amount of a substance. Then divide the previous amount by half each week until you get to 4 weeks. |
| # of Half Lives |
Time |
Amount |
| 0 |
0 |
1200 g |
| 1 |
1 week |
600 g |
| 2 |
2 weeks |
300 g |
| 3 |
3 weeks |
150 g |
| 4 |
4 weeks |
75 g |
After 4 weeks 75 grams of 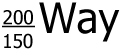 remains. 1125 grams of the daughter particle remain, (1200-75 = 1125.) remains. 1125 grams of the daughter particle remain, (1200-75 = 1125.) |
|
| |
|
|