One of the ways cause and effect is better understood is by modeling the behavior with a math equation. To generate a math equation from a collection of data, we will use a process called "linearizing data."

In this physics course there are three types of graphs that our labs data will generate. They are

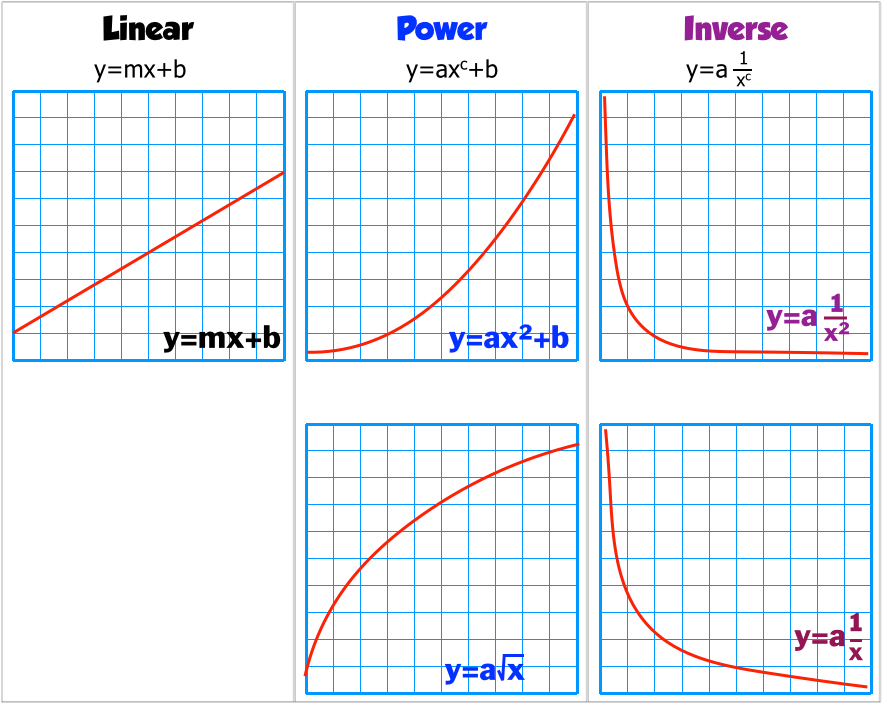
You need to recognize the graph types by their appearance. Unfortunately, the inverse graphs look similar. The inverse squared form has a curve that bends closer to the origin. Only by linearizing the data would you know that the function is either 1/x or 1/x².

There are a few ways to determine line that best represents a collections of data. We use the least squares method. Below is a collection of data points and the line of best fit.

The line of best fit provides a math model to make predictions about data points not on the graph and to evaluate the math model's precision. This math model yields an equation for a straight line in the form of "y = mx + b." Most programs interpret the data to give you the value for the slope and intercept.

The trendline function is Google Sheets can give you the slope and y-intercept.

There are two ways to evaluate if the y=mx+b that is derived from the line of best fit is close to representing the data.

1	The software calculates a value called the Regression coefficient, "R." The closer the absolute value of "R" is to 1, the better the fit of the trendline.
2	Use your brain and look at the data points. The line of best fit should closely follow about 70% or more the data points.

This 94 second video explains how to go from y = mx + b to an equation with the variables we use in science.

Below are examples of what the language looks like for each relationship. It generally fits this form,

(Vertical axis) is (type of proportionality) to the (horizontal axis.)

What the graph of raw data looks like	What the linearized data looks like & its equation.	Description in words
Linear
		Force is directly proportional to the time.
Power
		Force is proportional to time squared.
Inverse
		Force is proportional to the inverse of time.
Inverse squared
		Force is proportional to the inverse square of time.
Squareroot
		Force is proportional to the squareroot of time

We will be using Google Sheets to analyze data. See a short video below to see how to do some basic data manipulation in Sheets.

This video can be found on YouTube at https://youtu.be/5k5iNEjGnR.

Below is another video showing how to use Google's Sheets to Linearize data by finding the trendline. (This can be done in Excel but we use Google sheets because of its collaboration abilities.)

This video can be found on YouTube at https://youtu.be/qUQ5ApPQ3lU

You can also click here to see written instructions on how to get a "trendline" in "Google Sheets." (It will open in a new page.)

Click here to see a video example of how to do it using LoggerPro 3.8x. (AHS is currently not using LoggerPro for analysis.)

Sometimes when you insert a chart in Google Spreadsheets, you will not be able to create a trendline because you have 2 sets of data points on your screen instead of 1. This video will show you how to quickly fix that problem.

This video can be found on YouTube at https://youtu.be/YBH7NvKci8I