|
|
Page 6 
|
| This text is meant to accompany class discussions. It is not everything there is to know about uniform circular motion. It is meant as a prep for class. More detailed notes and examples are given in the class notes, presentations, and demonstrations (click here.) |
 |
Click for the questions that go with this reading |
More Significant Figure Rules |
| 5. |
Trailing zeros left of the decimal point are ambiguous.
These trailing zeros are also called "placeholders." They slide the other number around. In doing so they show how large the other numbers are. For example 6 hundred is written as 600. The, "00," push the 6 to the left showing how large the number is. Zeros that are place holders are NEVER significant. This rule is only for numbers larger than 9 that do not have any digits after the decimal.
Because of the way scientific notation is written, all of the number in scientific notation are significant. The last digit is the estimated digit.
|
| |
| Examples |
The zeros that are placeholders are highlighted in yellow. |
| 10 |
1 sig. fig. |
10: "0" on the right is a placeholder. The "1" is the only significant figure and it is the estimated measurement too. |
| 300 |
1 sig. fig. |
300: "00" on the right is a placeholder. The "3" is the only significant figure and it is the estimated measurement too. |
| 640 |
2 sig. figs. |
640: "0" on the right is a placeholder. The "64" are the only significant figures. The "4" is the estimated measurement. |
| 40030 |
4 sig. figs. |
40030: The"0" to the right of the "3" is a placeholder. The 4003 are significant and the 3 is the estimated measurement. |
| 304 000 |
3 sig. figs. |
304000: The "000" are placeholders. The 304 are the significant figures. The ) between the 3 and 4 are "bookends" to the lone 0. The 4 is the estimated number. |
| 90200 |
3 sig. figs. |
90200: The "00" to the right of the "2" are placeholders. The "902" are the significant figures and the 2 is the estimated measurement. |
| 3.0920 x 10-8 |
5 sig. figs. |
There are no placeholders in scientific notation. Every digit is significant in scientific notation. The digit farthest to the right is the estimated measurement. In this number it is the zero after the "2." |
|
| |
 |
| How many significant figures are in each number shown below? (Get a scrap piece of of paper and write your answer down before checking.) |
| 3050 |
|
1 900 030 |
|
4008 |
|
| 60 000 |
|
40 |
|
901 |
|
| 9030 |
|
9 020 000 |
|
5 006 000 |
|
| 10 040 |
|
50 010 |
|
750 |
|
| 9.500 x 102 |
|
7.01x106 |
|
|
|
|
|
| 6. |
Placing a decimal after a zero makes the zero significant. this is also indicated by placing a line over that zero.
As written, the number 46 000. Has two significant figures. It implies that the "6" is the estimated part of the measurement. But suppose the instrument used for making this measurement measured to the one's place. There are three ways to indicate that the last zero, in the one's place, is the estimated number in the measurement
- Write the number in scientific notation, " 4.6000 x 104 "
- Place a decimal after the number. " 46 000. "
- Draw a line over the zero that is estimated, "
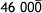 " "
|
| |
| Examples |
| 500. |
3 sig. figs. |
500: The last zero is estimated number |
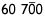 |
4 sig. figs. |
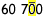 : The zero after the "7" is the estimated number.. : The zero after the "7" is the estimated number.. |
| 4.50x102 |
3 sig. figs. |
4.50x102: Because zeros after the decimal are significant, the last zero is the estimated measurement. |
| Note: |
| Calculators and computers cannot always show exponents. When this happens they will use the shortcut of replacing the "x10" with an "e" or an "E." Calculators do this to conserve screen space. You are not to use the "E" notation on anything that is to be read by someone else. It is improper form. |
|
| |
| Exact Numbers |
Counting numbers are exact numbers with an infinite number of significant figures. Numbers like a dozen, a gross, a half, double, triple, etcetera, are counting numbers and do not have a specified number of significant figures or an estimated number. Assuming the number of students in a room was counted, it too is an exact number. The numbers of trials in an experiment are also counting a number. These do not contribute to errors when used in math expressions.
1 mile is defined as 5280 feet. Therefore 5280 is a perfect number and has an infinite number of significant digits. 1 meter is defined as 100 cm. Therefore 100 has an infinite number of significant digits. Defined quantities are perfect too, like counting numbers. However, it is important to know the origins of some definitions. For example 1 mile is also equal to 1609 meters. But this is not a definition, "1609" is a conversion and is a rounded number. Therefore 1609 has for significant digits where the "9" is estimated. |
 |
| For each number below pick the estimated number. (Get a scrap piece of paper and write your answer down before checking.) |
| 3.45 |
|
23.40 |
|
4500 |
|
| 0.008 |
|
5000 |
|
3.40 x 102 |
|
| 54 000 000 |
|
3.04 |
|
40 |
|
| 90.00 |
|
5607 |
|
8020 |
|
| 1.050 x 10-4 |
|
900 |
|
4060 |
|
| 603.0 |
|
50. |
|
0.00050 |
|
| 6.04 |
|
4.0 |
|
600. |
|
|
|
|
| |
|
|
|
|
|